Относительное изменение хорды оттяжки ε=ΔL/L связано с напряжением уравнением нити:

где P=p/A, Н/м^3 – поперечная нагрузка, Н/м, отнесенная к площади А, м^2; индекс "0" относится к величинам исходного состояния.
Примем за исходное состояние – состояние при температуре t и обозначим Δt=t-t0. При изменении температуры ствол деформируется на величину α·Δt, что повлечет за собой изменение длины оттяжки на ΔL = α·Δt·(sinβ)^2, где β – угол наклона оттяжки к горизонту. С изменением температуры поперечная нагрузка (собственный вес) не меняется, поэтому можно принять:
P = P0 = γ = g·cosβ /A,
где g – погонный вес, Н/м; А – площадь ванты.
Подставляя указанные величины в уравнение нити и производя преобразования, получаем разрешающее уравнение, позволяющее скорректировать напряжение с учетом изменения температуры:


где P=p/A, Н/м^3 – поперечная нагрузка, Н/м, отнесенная к площади А, м^2; индекс "0" относится к величинам исходного состояния.
Примем за исходное состояние – состояние при температуре t и обозначим Δt=t-t0. При изменении температуры ствол деформируется на величину α·Δt, что повлечет за собой изменение длины оттяжки на ΔL = α·Δt·(sinβ)^2, где β – угол наклона оттяжки к горизонту. С изменением температуры поперечная нагрузка (собственный вес) не меняется, поэтому можно принять:
P = P0 = γ = g·cosβ /A,
где g – погонный вес, Н/м; А – площадь ванты.
Подставляя указанные величины в уравнение нити и производя преобразования, получаем разрешающее уравнение, позволяющее скорректировать напряжение с учетом изменения температуры:
или
где
Действительный корень уравнения определяется формулой:
Определив
из уравнения величину напряжения при заданном перепаде температур
определяем как обычно - умножением напряжения на площадь.
Указанная методика рекомендована в книге
Petersen, Chr. (1970): Guyed masts and chimneys, Verlag Ernst & Sohn, Berlin-München-Düsseldorf, Germany.
Ниже приведен код пользовательской функции для OOo Calc
Function otemp(T, T0, N0, A, g, E, L, beta, h)
' Возвращает тяжение стальной оттяжки мачты, тс, при заданной темературе T
'Описание величин
't = Заданная температура
'T0 - Начальная температура (среднегодовая температура воздуха)
'N0 - Начальное тяжение ванты, тс, при температуре T0
'A = Площадь оттяжки, мм2
'g = Погонный вес отттяжки, кгс/м
'E = Модуль Юнга оттяжки, кгс/см2
'L = Длина оттяжки, м
'beta = Угол наклона оттяжки к горизонту в градусах
'h = Высота ствола под оттяжкой
'Переобозначение переменных и перевод всех величин в систему кгс, см, рад.
N0=N0*1000
A=A/100
g=g/100
L=L*100
beta = beta*3.1416/180
h=h*100
alpha = 0.000012
Gamma = g * Cos(beta) / A
Gamma = g * Cos(beta) / A
Delta = t - T0
s0 = N0 / A
C = Gamma ^ 2 * L ^ 2 * E / (24 * s0 ^ 3)
B = (1 - C - alpha * Delta * E * (1 - (h / L) * Sin(beta)) / s0)
z = 1 / 6 * (108 * C + 8 * B ^ 3 + 12 * Sqr(81 * C ^ 2 + 12 * C * B ^ 3)) ^ (1 / 3) + 2 / 3 * B ^ 2 / ((108 * C + 8 * B ^ 3 + 12 * Sqr(81 * C ^ 2 + 12 * C * B ^ 3)) ^ (1 / 3)) + 1 / 3 * B
'Искомое усилия тяжения в тс
z = 1 / 6 * (108 * C + 8 * B ^ 3 + 12 * Sqr(81 * C ^ 2 + 12 * C * B ^ 3)) ^ (1 / 3) + 2 / 3 * B ^ 2 / ((108 * C + 8 * B ^ 3 + 12 * Sqr(81 * C ^ 2 + 12 * C * B ^ 3)) ^ (1 / 3)) + 1 / 3 * B
'Искомое усилия тяжения в тс
N = z * s0 * A / 1000
otemp = N
End Function
otemp = N
End Function
Пример использования функции:

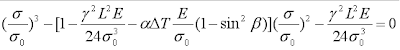
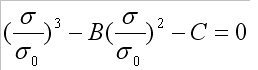


No comments:
Post a Comment